OBJETIVOS:
Observación y cálculo del efecto de resonancia. Circuitos resonantes serie y paralelo. Efectos y particularidades de cada uno de ellos. Cálculo de Xc y Xl a distintas frecuencias.
CONOCIMIENTOS PREVIOS:
RESONANCIA
Un circuito de resonancia está compuesto por una resistencia un condensador y una bóbina en el cual se alimentan de corriente alterna. Hay dos tipos de circuitos resonantes; uno es el circuito resonantes serie y el otro es el circuito resonante paralelo. Cuando a la entrada del circuito se le aplica una frecuencia el circuito reaccionará de una forma distinta.
La reactancia de un condensador o de una bobina es el valor óhmico que se opone al paso de electrónes. Cuando la frecuencia crece la reactancia de la bobina aumenta, en tanto que al del condensador disminuye. Pero hay una determinada frecuencia que la cual los valores absolutos de ambas reactancias se iguala y a este fenómeno se llama «Frecuencia de resonancia». Su valor se deduce de esta manera:
XL = 2 · p · F · L XC = 1 =
2 · p · F · C
Para la frecuencia de resonancia:
F = 1 =
2p L·C
El factor de calidad es algo más amplio, puede definirse en el caso de una bobina, como la reación:
Q = XL
RL
Hay un concepto mas que es el ancho de banda que es el margen de frecuencias.
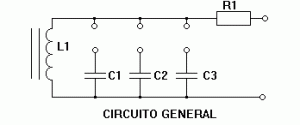
esquemas:
MATERIAL NECESARIO:
– Osciloscopio de doble haz.
– Generador de baja frecuencia.
– Polímetro digital o analógico.
– Placa de ensayo de circuitos resonantes compuesta de C1 = 3,9nF C2 = 1,8nF
C3 = 1000 pF. y una resistencia R1 = 1KW .
MÉTODO OPERATIVO:
Realizar los ejercicios tanto los del circuito resonante en serie como los del circuito resonante paralelo. Sacar conclusiones.
PRÁCTICAS PROPUESTAS:
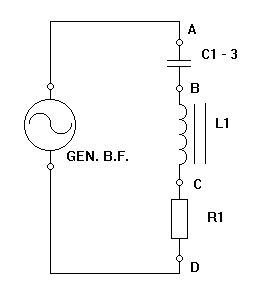
CIRCUITO RESONANTE SERIE
1.- Realizar con el genrador de B.F. y en onda senoidal, un barrido de frecuencias según tabla 1 e ir mediendo la intensidad que circula por el condensador en cada frecuencia, vigilando al mismo tiempo, mediante el osciloscopio entre extremos del condensador que la tensión se mantenga constante; si ésta varía en algún momento se retocaría el mando de amplitud del generador de B.F. para corregirlo.
Al hacer el cálculo de Xc debemos tener en cuenta que la tensión la medimos con el osciloscopio ( Vpp ) y la corriente con el polímetro ( Ief ), por lo tanto, debemos pasar la tensión a eficaz.
C1
| FREC. (KHz) | I (mA) | Xc (KW ) | FREC. (Hz) | I (mA) | Xc (KW ) |
| 0 | 0,1 | 35 | 1,77 | 0,4 | |
| 5 | 0,27 | 2,6 | 38 | 1,81 | 0,38 |
| 6 | 0,32 | 2,18 | 40 | 1,87 | 0,37 |
| 7 | 0,37 | 1,9 | 42 | 1,93 | 0,36 |
| 8 | 0,43 | 1,62 | 45 | 2 | 0,35 |
| 9 | 0,47 | 1,48 | 48 | 2,08 | 0,33 |
| 10 | 0,52 | 1,34 | 50 | 2,25 | 0,31 |
| 12 | 0,62 | 1,13 | 52 | 2,28 | 0,3 |
| 15 | 0,77 | 1 | 55 | 2,33 | 0,3 |
| 18 | 0,88 | 0,8 | |||
| 20 | 1 | 0,7 | |||
| 22 | 1,11 | 0,63 | |||
| 25 | 1,3 | 0,53 | |||
| 28 | 1,42 | 0,5 | |||
| 30 | 1,57 | 0,44 |
C2
| FREC. (KHz) | I (mA) | Xc (KW ) | FREC. (Hz) | I (mA) | Xc (KW ) |
| 0 | 0,08 | 8,75 | 35 | 0,76 | 1 |
| 5 | 0,13 | 5,38 | 38 | 0,82 | 0,85 |
| 6 | 0,15 | 4,66 | 40 | 0,84 | 0,83 |
| 7 | 0,17 | 4,11 | 42 | 0,89 | 0,78 |
| 8 | 0,2 | 3,5 | 45 | 0,97 | 0,72 |
| 9 | 0,22 | 3,18 | 48 | 1,02 | 0,68 |
| 10 | 0,24 | 2,91 | 50 | 1,06 | 0,66 |
| 12 | 0,29 | 2,41 | 52 | 1,08 | 0,64 |
| 15 | 0,35 | 2 | 55 | 1,12 | 0,62 |
| 18 | 0,4 | 1,75 | |||
| 20 | 0,45 | 1,55 | |||
| 22 | 0,49 | 1,42 | |||
| 25 | 0,55 | 1,27 | |||
| 28 | 0,63 | 1,11 | |||
| 30 | 0,67 | 1 |
C3
| FREC. (KHz) | I (mA) | Xc (KW ) | FREC. (Hz) | I (mA) | Xc (KW ) |
| 0 | 0,02 | 35 | 35 | 0,4 | 1,75 |
| 5 | 0,07 | 10 | 38 | 0,42 | 1,66 |
| 6 | 0,08 | 8,75 | 40 | 0,44 | 1,6 |
| 7 | 0,09 | 7,7 | 42 | 0,46 | 1,52 |
| 8 | 0,1 | 7 | 45 | 0,48 | 1,45 |
| 9 | 0,12 | 5,83 | 48 | 0,5 | 1,4 |
| 10 | 0,13 | 5,38 | 50 | 0,52 | 1,34 |
| 12 | 0,15 | 4,66 | 52 | 0,54 | 1,29 |
| 15 | 0,18 | 3,88 | 55 | 0,57 | 1,28 |
| 18 | 0,21 | 3,33 | |||
| 20 | 0,23 | 3,04 | |||
| 22 | 0,25 | 2,8 | |||
| 25 | 0,28 | 2,5 | |||
| 28 | 0,31 | 2,25 | |||
| 30 | 0,33 | 2,12 |
L
| FREC. (KHz) | I (mA) | Xc (KW ) | FREC. (Hz) | I (mA) | Xc (W ) |
| 0 | 6,63 | 0,10 | 35 | 0,51 | 1,37 |
| 5 | 5,07 | 0,13 | 38 | 0,42 | 1,66 |
| 6 | 4,29 | 0,16 | 40 | 0,39 | 1,8 |
| 7 | 3,57 | 0,19 | 42 | 0,34 | 2,05 |
| 8 | 3,17 | 0,22 | 45 | 0,29 | 2,41 |
| 9 | 2,84 | 0,24 | 48 | 0,23 | 3,04 |
| 10 | 2,51 | 0,27 | 50 | 0,19 | 3,68 |
| 12 | 2,06 | 0,34 | 52 | 0,17 | 4,11 |
| 15 | 1,62 | 0,43 | 55 | 0,12 | 5,83 |
| 18 | 1,32 | 0,53 | |||
| 20 | 1,15 | 0,6 | |||
| 22 | 1 | 0,7 | |||
| 25 | 0,85 | 0,82 | |||
| 28 | 0,72 | 0,97 | |||
| 30 | 0,65 | 1 |
2.- Estando el circuito en resonancia, medir mediante el osciloscopio la tensión proporcionada por el generador, entre extremos de la bobina y entre extremos del condensador , anotarlas en la siguiente tabla.
| V. entrada | V R1 | VL1 | VC1-3 | Frec. reson. | |
| C1 | 1,6 Vpp | 1,4 Vpp | 2,6 Vpp | 2,4 Vpp | 22 KHz |
| C2 | 1,4 Vpp | 1,4 Vpp | 2,6 Vpp | 3 Vpp | 30 KHz |
| C3 | 1,4 Vpp | 1,4 Vpp | 2,6 Vpp | 3,8 Vpp | 38 KHz |
3.- A la frecuencia de resonancia, y mediante las figuras de Lissajous, medir el desfasaje entre las tenciones en el condensador y la bobina. Conectar el eje Y del osciloscopio al punto A y el eje X al punto B (Punto D a masa). Calcularlo y anotarlo en la siguiente tabla.
C1 sen a = +- B = 1 = 0,71
A 1,4
C2 sen a = +- B = 1,4 = 0,77
A 1,8
C3 sen a = +- B = 1,1 = 0,78
A 1,4
| Frec. resonancia | Desfasaje | |
| C1 | 22.000 Hz | 0,71 |
| C2 | 30.000 Hz | 0,77 |
| C3 | 38.000 Hz | 0,78 |
4.- Sabiendo la Xl de la bobina, calcular su inductancia L a las tres frecuencias de resonancia. Rellenar la tabla correspondiente conlos valores obtenidos.
NOTA.- Teóricamente, la inductancia de la bobina no debe variar con la frecuencia, pero debido al núcleo de ferrita, sí varía, por lo tanto, debemos calcularla en los tres casos de resonancia serie.
L = XL
2 · p · F
| Frec. Resonancia. (Hz) | L ( Henrios ) | C ( Faradios ) | |
| C1 | 22000 | 0,0050 | 3,9 · 10-9 |
| C2 | 30000 | 0,0053 | 1,8 · 10-9 |
| C3 | 38000 | 0,0069 | 1000 · 10-12 |
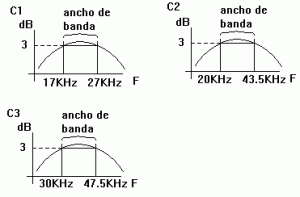
5.- Midiendo la caída de tensión enla resistencia R1, hacer un barrido de frecuencias por encima y por debajo de la frecuencia de resonancia para obtener el ancho de banda del ciurcuito. ( Caída de -3dB de la tensión en extremos de R1 ).
2 Vpp – 3dB = 0,7 Vpp
| Fi | Fs | |
| C1 | 17.000 Hz | 27.000 Hz |
| C2 | 20.000 Hz | 43.500 Hz |
| C3 | 30.000 Hz | 47.000 Hz |
6.- Anotar en la siguiente tabla la frecuencia calculada, la frecuencia de la curva y la frecuencia real.
| Frecuencia calculada | Frecuencia de la curva | Frecuencia real | |
| C1 | 36 KHz | 22 KHz | 22 KHz |
| C2 | 51 KHz | 30 KHz | 30 KHz |
| C3 | 60,5 KHz | 38 KHz | 38 KHz |
F1 = 1 = 1 = 36 KHz
2p L·C 2p 0,005·3,9·10-9
F2 = 1 = 1 = 51 KHz
2p L·C 2p 0,0053·1,8·10-9
F3 = 1 = 1 = 60,5 KHz
2p L·C 2p 0,0069·1000·10-12
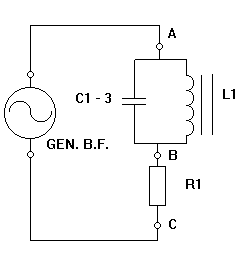
CIRCUITO RESONANTE PARALELO
7.- Haciendo un barrido de frecuencias y midiendo la caída de tensión en R1 mediante el osciloscopio, comprobar la frecuencia de resonancia. Medir la corriente que pasa a través de R1 cuando el circuito está en resonancia.
| Frecuencia de resonancia | Intensidad (mA) | XL (W ) | |
| C1 | 20 KHz | 0,95 | 0,73 K |
| C2 | 27 KHz | 0,93 | 0,752 K |
| C3 | 37 KHz | 0,91 | 0,76 K |
8.- Realizar la siguiente tabla:
| Frecuencia de resonancia | L ( Henrios ) | C ( Faradios ) | |
| C1 | 20.000 Hz | 0,0058 | 3,9 · 10-9 |
| C2 | 27.000 Hz | 0,0053 | 1,8 · 10-9 |
| C3 | 37.000 Hz | 0,0069 | 1000 · 10-12 |
9.- Estando el circuito en resonancia, medir en extremos del generador, en extremos del circuito resonante y en extremos de la resistencia R1. ( Con el osciloscopio ). Anotar las tensiones.
| V. entrada | V.AB | VR1 | |
| C1 | 1,9 Vpp | 2 Vpp | 0,02 Vpp |
| C2 | 1,9 Vpp | 2 Vpp | 0,08 Vpp |
| C3 | 2 Vpp | 1,9 Vpp | 0,015 Vpp |
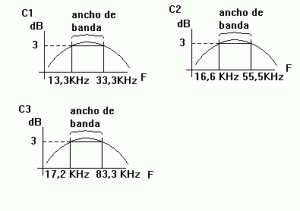
10.- Al igual que en el circuito resonante serie, y mediendo la caída de tensión de -3dB en R1 hacer un barrido de frecuencias por encima y por debajo de la de resonancia para obtener el ancho de banda del circuito.
| Fi | Fs | |
| C1 | 13,3 KHz | 33,3 KHz |
| C2 | 16,6 KHz | 55,5 KHz |
| C3 | 17,2 KHz | 83,3 KHz |
11.- Rellena la siguiente tabla de frecuencias.
| Frecuencia calculada | Frecuencia de la curva | Frecuencia real | |
| C1 | 35,3 KHz | 22 KHz | 20 KHz |
| C2 | 52 KHz | 30 KHz | 27 KHz |
| C3 | 88 KHz | 38 KHz | 37 KHz |
F1 = 1 = 1 = 35,3 KHz
2p L·C 2p 0,0058·3,9·10-9
F2 = 1 = 1 = 52 KHz
2p L·C 2p 0,0044·1,8·10-9
F3 = 1 = 1 = 88 KHz
2p L·C 2p 0,0032·1000·10-12
observaciones:
Para averiguar la frecuencia de resonancia en el circuito de resonancia serie, había que hacer un barrido de frecuencias mediendo al mismo tiempo la tensión en R1, y para saber la frecuencia de resonancia tenía que tener R1 la máxima tensión y en el circuito de resonancia paralelo tenía que tener en R1 la mínima tensión.
Cuando el circuito entraba en resonancia, tanto el de serie como el de paralelo, la tensión en la bobina es la misma tensión del condensador, entonces eso quiere decir que el valor óhmico se iguala ( XL = XC ).
Al realizar los cálculos de la frecuencia nos hemos dado cuenta de que nos saría diferentes valores de frecuencia y parece ser debido a la ( L ) de la bobina que varía bastante de la teórica a la práctica.